Una lista es una estructura de datos secuencial.
Una manera de clasificarlas es por la forma de acceder al siguiente elemento:
- lista densa: la propia estructura determina cuál es el siguiente elemento de la lista. Ejemplo: un array.
- lista enlazada: la posición del siguiente elemento de la estructura la determina el elemento actual. Es necesario almacenar al menos la posición de memoria del primer elemento. Además es dinámica, es decir, su tamaño cambia durante la ejecución del programa.
- lista enlazada: la posición del siguiente elemento de la estructura la determina el elemento actual. Es necesario almacenar al menos la posición de memoria del primer elemento. Además es dinámica, es decir, su tamaño cambia durante la ejecución del programa.
Una lista enlazada se puede definir recursivamente de la siguiente manera:
- una lista enlazada es una estructura vacía o
- un elemento de información y un enlace hacia una lista (un nodo).
- un elemento de información y un enlace hacia una lista (un nodo).
Gráficamente se suele representar así:

Como se ha dicho anteriormente, pueden cambiar de tamaño, pero su ventaja fundamental es que son flexibles a la hora de reorganizar sus elementos; a cambio se ha de pagar una mayor lentitud a la hora de acceder a cualquier elemento.
En la lista de la figura anterior se puede observar que hay dos elementos de información, x e y. Supongamos que queremos añadir un nuevo nodo, con la información p, al comienzo de la lista. Para hacerlo basta con crear ese nodo, introducir la información p, y hacer un enlace hacia el siguiente nodo, que en este caso contiene la información x.
¿Qué ocurre si quisiéramos hacer lo mismo sobre un array?. En ese caso sería necesario desplazar todos los elementos de información "hacia la derecha", para poder introducir el nuevo elemento, una operación muy engorrosa.
¿Qué ocurre si quisiéramos hacer lo mismo sobre un array?. En ese caso sería necesario desplazar todos los elementos de información "hacia la derecha", para poder introducir el nuevo elemento, una operación muy engorrosa.
Implementación
Para representar en lenguaje C esta estructura de datos se utilizarán punteros, un tipo de datos que suministra el lenguaje. Se representará una lista vacía con la constante NULL. Se puede definir la lista enlazada de la siguiente manera:
struct lista
{
int clave;
struct lista *sig;
};
Como se puede observar, en este caso el elemento de información es simplemente un número entero. Además se trata de una definición autorreferencial. Pueden hacerse definiciones más complejas. Ejemplo:
struct cl
{
char nombre[20];
int edad;
};
struct lista
{
struct cl datos;
int clave;
struct lista *sig;
};
Cuando se crea una lista debe estar vacía. Por tanto para crearla se hace lo siguiente:
struct lista *L; L = NULL;
- Inserción al comienzo de una lista:
Es necesario utilizar una variable auxiliar, que se utiliza para crear el nuevo nodo mediante la reserva de memoria y asignación de la clave. Posteriormente es necesario reorganizar los enlaces, es decir, el nuevo nodo debe apuntar al que era el primer elemento de la lista y a su vez debe pasar a ser el primer elemento.
En el siguiente ejemplo se muestra un programa que crea una lista con cuatro números. Notar que al introducir al comienzo de la lista, los elementos quedan ordenados en sentido inverso al de su llegada. Notar también que se ha utilizado un puntero auxiliar p para mantener correctamente los enlaces dentro de la lista.
En el siguiente ejemplo se muestra un programa que crea una lista con cuatro números. Notar que al introducir al comienzo de la lista, los elementos quedan ordenados en sentido inverso al de su llegada. Notar también que se ha utilizado un puntero auxiliar p para mantener correctamente los enlaces dentro de la lista.
#include <stdlib.h>
struct lista
{
int clave;
struct lista *sig;
};
int main(void)
{
struct lista *L;
struct lista *p;
int i;
L = NULL; /* Crea una lista vacia */
for (i = 4; i >= 1; i--)
{
/* Reserva memoria para un nodo */
p = (struct lista *) malloc(sizeof(struct lista));
p->clave = i; /* Introduce la informacion */
p->sig = L; /* reorganiza */
L = p; /* los enlaces */
}
return 0;
}
- Recorrido de una lista.
La idea es ir avanzando desde el primer elemento hasta encontrar la lista vacía. Antes de acceder a la estructura lista es fundamental saber si esa estructura existe, es decir, que no está vacía. En el caso de estarlo o de no estar inicializada es posible que el programa falle y sea difícil detectar donde, y en algunos casos puede abortarse inmediatamente la ejecución del programa, lo cual suele ser de gran ayuda para la depuración.
Como se ha dicho antes, la lista enlazada es una estructura recursiva, y una posibilidad para su recorrido es hacerlo de forma recursiva. A continuación se expone el código de un programa que muestra el valor de la clave y almacena la suma de todos los valores en una variable pasada por referencia (un puntero a entero). Por el hecho de ser un proceso recursivo se utiliza un procedimiento para hacer el recorrido. Nótese como antes de hacer una operación sobre el elemento se comprueba si existe.
Como se ha dicho antes, la lista enlazada es una estructura recursiva, y una posibilidad para su recorrido es hacerlo de forma recursiva. A continuación se expone el código de un programa que muestra el valor de la clave y almacena la suma de todos los valores en una variable pasada por referencia (un puntero a entero). Por el hecho de ser un proceso recursivo se utiliza un procedimiento para hacer el recorrido. Nótese como antes de hacer una operación sobre el elemento se comprueba si existe.
int main(void)
{
struct lista *L;
struct lista *p;
int suma;
L = NULL;
/* crear la lista */
...
suma = 0;
recorrer(L, &suma);
return 0;
}
void recorrer(struct lista *L, int *suma)
{
if (L != NULL) {
printf("%d, ", L->clave);
*suma = *suma + L->clave;
recorrer(L->sig, suma);
}
}
Sin embargo, a la hora de hacer un programa, es más eficaz si el recorrido se hace de forma iterativa. En este caso se necesita una variable auxiliar que se desplace sobre la lista para no perder la referencia al primer elemento. Se expone un programa que hace la misma operación que el anterior, pero sin recursión.
int main(void)
{
struct lista *L;
struct lista *p;
int suma;
L = NULL;
/* crear la lista */
...
p = L;
suma = 0;
while (p != NULL) {
printf("%d, ", p->clave);
suma = suma + p->clave;
p = p->sig;
}
return 0;
}
A menudo resulta un poco difícil de entender la instrucción p = p->sig; Simplemente cambia la dirección actual del puntero p por la dirección del siguiente enlace. También es común encontrar instrucciones del estilo: p = p->sig->sig; Esto puede traducirse en dos instrucciones, de la siguiente manera:
p = p->sig;
p = p->sig;
Obviamente sólo debe usarse cuando se sepa que p->sig es una estructura no vacía, puesto que si fuera vacía, al hacer otra vez p = p->sig se produciría una referencia a memoria no válida.
p = p->sig;
p = p->sig;
Obviamente sólo debe usarse cuando se sepa que p->sig es una estructura no vacía, puesto que si fuera vacía, al hacer otra vez p = p->sig se produciría una referencia a memoria no válida.
¿Y si queremos insertar en una posición arbitraria de la lista o queremos borrar un elemento? Como se trata de operaciones algo más complicadas (tampoco mucho) se expone su desarrollo y sus variantes en los siguientes tipos de listas: las listas ordenadas y las listas reorganizables. Asimismo se estudiarán después las listas que incorporan cabecera y centinela. También se estudiarán las listas con doble enlace. Todas las implementaciones se harán de forma iterativa, y se deja propuesta por ser más sencilla su implementación recursiva, aunque es recomendable utilizar la versión iterativa.
Las listas ordenadas son aquellas en las que la posición de cada elemento depende de su contenido. Por ejemplo, podemos tener una lista enlazada que contenga el nombre y apellidos de un alumno y queremos que los elementos -los alumnos- estén en la lista en orden alfabético.
La creación de una lista ordenada es igual que antes:
struct lista *L; L = NULL;
Cuando haya que insertar un nuevo elemento en la lista ordenada hay que hacerlo en el lugar que le corresponda, y esto depende del orden y de la clave escogidos. Este proceso se realiza en tres pasos:
1.- Localizar el lugar correspondiente al elemento a insertar. Se utilizan dos punteros: anterior y actual, que garanticen la correcta posición de cada enlace.
2.- Reservar memoria para él (puede hacerse como primer paso). Se usa un puntero auxiliar (nuevo) para reservar memoria.
3.- Enlazarlo. Esta es la parte más complicada, porque hay que considerar la diferencia de insertar al principio, no importa si la lista está vacía, o insertar en otra posición. Se utilizan los tres punteros antes definidos para actualizar los enlaces.
1.- Localizar el lugar correspondiente al elemento a insertar. Se utilizan dos punteros: anterior y actual, que garanticen la correcta posición de cada enlace.
2.- Reservar memoria para él (puede hacerse como primer paso). Se usa un puntero auxiliar (nuevo) para reservar memoria.
3.- Enlazarlo. Esta es la parte más complicada, porque hay que considerar la diferencia de insertar al principio, no importa si la lista está vacía, o insertar en otra posición. Se utilizan los tres punteros antes definidos para actualizar los enlaces.
A continuación se expone un programa que realiza la inserción de un elemento en una lista ordenada. Suponemos claves de tipo entero ordenadas ascendentemente.
#include <stdio.h>
#include <stdlib.h>
struct lista
{
int clave;
struct lista *sig;
};
/* prototipo */
void insertar(struct lista **L, int elem);
int main(void)
{
struct lista *L;
L = NULL; /* Lista vacia */
/* para probar la insercion se han tomado 3 elementos */
insertar(&L, 0);
insertar(&L, 1);
insertar(&L, -1);
return 0;
}
void insertar(struct lista **L, int elem)
{
struct lista *actual, *anterior, *nuevo;
/* 1.- se busca su posicion */
anterior = actual = *L;
while (actual != NULL && actual->clave < elem) {
anterior = actual;
actual = actual->sig;
}
/* 2.- se crea el nodo */
nuevo = (struct lista *) malloc(sizeof(struct lista));
nuevo->clave = elem;
/* 3.- Se enlaza */
if (anterior == NULL || anterior == actual) { /* inserta al principio */
nuevo->sig = anterior;
*L = nuevo; /* importante: al insertar al principio actuliza la cabecera */
}
else { /* inserta entre medias o al final */
nuevo->sig = actual;
anterior->sig = nuevo;
}
}
Se puede apreciar que se pasa la lista L con el parámetro **L . La razón para hacer esto es que cuando se inserta al comienzo de la lista (porque está vacía o es donde corresponde) se cambia la cabecera.
Un ejemplo de prueba: suponer que se tiene esta lista enlazada: 1 -> 3 -> 5 -> NULL
Queremos insertar un 4. Al hacer la búsqueda el puntero actual apunta al 5. El puntero anterior apunta al 3. Y nuevo contiene el valor 4. Como no se inserta al principio se hace que el enlace siguiente a nuevo sea actual, es decir, el 5, y el enlace siguiente a anterior será nuevo, es decir, el 4.
La mejor manera de entender el funcionamiento es haciendo una serie de seguimientos a mano o con la ayuda del depurador.
Queremos insertar un 4. Al hacer la búsqueda el puntero actual apunta al 5. El puntero anterior apunta al 3. Y nuevo contiene el valor 4. Como no se inserta al principio se hace que el enlace siguiente a nuevo sea actual, es decir, el 5, y el enlace siguiente a anterior será nuevo, es decir, el 4.
La mejor manera de entender el funcionamiento es haciendo una serie de seguimientos a mano o con la ayuda del depurador.
A continuación se explica el borrado de un elemento. El procedimiento consiste en localizarlo y borrarlo si existe. Aquí también se distingue el caso de borrar al principio o borrar en cualquier otra posición. Se puede observar que el algoritmo no tiene ningún problema si el elemento no existe o la lista está vacía.
void borrar(struct lista **L, int elem)
{
struct lista *actual, *anterior;
/* 1.- busca su posicion. Es casi igual que en la insercion, ojo al (<) */
anterior = actual = *L;
while (actual != NULL && actual->clave < elem) {
anterior = actual;
actual = actual->sig;
}
/* 2.- Lo borra si existe */
if (actual != NULL && actual->clave == elem) {
if (anterior == actual) /* borrar el primero */
*L = actual->sig; /* o tambien (*L)->sig; */
else /* borrar en otro sitio */
anterior->sig = actual->sig;
free(actual);
}
}
Ejemplo: para borrar la clave '1' se indica así: borrar(&L, 1);
Las listas reorganizables son aquellas en las que cada vez que se accede a un elemento éste se coloca al comienzo de la lista. Si el elemento al que se accede no está en la lista entonces se añade al comienzo de la misma. Cuando se trata de borrar un elemento se procede de la misma manera que en la operación de borrado de la lista ordenada. Notar que el orden en una lista reorganizable depende del acceso a un elemento, y no de los valores de las claves.
No se va a desarrollar el procedimiento de inserción / acceso en una lista, se deja como ejercicio. De todas formas es sencillo. Primero se busca ese elemento, si existe se pone al comienzo de la lista, con cuidado de no perder los enlaces entre el elemento anterior y el siguiente. Y si no existe pues se añade al principio y ya está. Por último se actualiza la cabecera.
Como se ha observado anteriormente, a la hora de insertar o actualizar elementos en una lista ordenada o reorganizable es fundamental actualizar el primer elemento de la lista cuando sea necesario. Esto lleva un coste de tiempo, aunque sea pequeño salvo en el caso de numerosas inserciones y borrados. Para subsanar este problema se utiliza la cabecera ficticia.
La cabecera ficticia añade un elemento (sin clave, por eso es ficticia) a la estructura delante del primer elemento. Evitará el caso especial de insertar delante del primer elemento. Gráficamente se puede ver así:
La cabecera ficticia añade un elemento (sin clave, por eso es ficticia) a la estructura delante del primer elemento. Evitará el caso especial de insertar delante del primer elemento. Gráficamente se puede ver así:
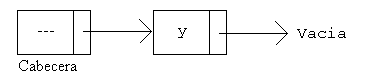
Se declara una lista vacía con cabecera, reservando memoria para la cabecera, de la siguiente manera:
struct lista {
int clave;
struct lista *sig;
}
...
struct lista *L;
L = (struct lista *) malloc(sizeof(struct lista));
L->sig = NULL;
Antes de implementar el proceso de inserción en una lista con cabecera, se explicará el uso del centinela, y se realizarán los procedimientos de inserción y borrado aprovechando ambas ideas.
El centinela es un elemento que se añade al final de la estructura, y sirve para acotar los elementos de información que forman la lista. Pero tiene otra utilidad: el lector habrá observado que a la hora de buscar un elemento de información, ya sea en la inserción o en el borrado, es importante no dar un paso en falso, y por eso se comprueba que no se está en una posición de información vacía. Pues bien, el centinela evita ese problema, al tiempo que acelera la búsqueda.
A la hora de la búsqueda primero se copia la clave que buscamos en el centinela, y a continuación se hace una búsqueda por toda la lista hasta encontrar el elemento que se busca. Dicho elemento se encontrará en cualquier posición de la lista, o bien en el centinela en el caso de que no estuviera en la lista. Como se sabe que el elemento está en algún lugar de la lista (aunque sea en el centinela) no hay necesidad de comprobar si estamos en una posición vacía.
Cuando la lista está vacía la cabecera apunta al centinela. El centinela siempre se apunta a si mismo. Esto se hace así por convenio.
Gráficamente se puede representar así:
Cuando la lista está vacía la cabecera apunta al centinela. El centinela siempre se apunta a si mismo. Esto se hace así por convenio.
Gráficamente se puede representar así:
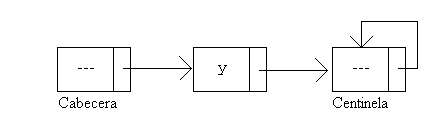
A continuación se realiza una implementación de lista enlazada ordenada, que incluye a la vez cabecera y centinela.
struct lista
{
int clave;
struct lista *sig;
};
/* lista con cabecera y centinela */
struct listacc
{
struct lista *cabecera,
*centinela;
};
Procedimiento de inicialización (nótese el *LCC):
void crearLCC(struct listacc *LCC)
{
LCC->cabecera = (struct lista *) malloc(sizeof(struct lista));
LCC->centinela = (struct lista *) malloc(sizeof(struct lista));
LCC->cabecera->sig = LCC->centinela;
LCC->centinela->sig = LCC->centinela; /* opcional, por convenio */
}
Procedimiento de inserción:
void insertarLCC(struct listacc LCC, int elem)
{
struct lista *anterior, *actual, *nuevo;
/* 1.- busca */
anterior = LCC.cabecera;
actual = LCC.cabecera->sig;
LCC.centinela->clave = elem;
while (actual->clave < elem) {
anterior = actual;
actual = actual->sig;
}
/* 2.- crea */
nuevo = (struct lista *) malloc(sizeof(struct lista));
nuevo->clave = elem;
/* 3.- enlaza */
nuevo->sig = actual;
anterior->sig = nuevo;
}
Procedimiento de borrado:
void borrarLCC(struct listacc LCC, int elem)
{
struct lista *anterior, *actual;
/* 1.- busca */
anterior = LCC.cabecera;
actual = LCC.cabecera->sig;
LCC.centinela->clave = elem;
while (actual->clave < elem) {
anterior = actual;
actual = actual->sig;
}
/* 2.- borra si existe */
if (actual != LCC.centinela && actual->clave == elem) {
anterior->sig = actual->sig;
free(actual);
}
}
Ejemplo de uso:
#include <stdio.h>
#include <stdlib.h>
struct lista
{
int clave;
struct lista *sig;
};
struct listacc
{
struct lista *cabecera,
*centinela;
};
void crearLCC(struct listacc *LCC);
void insertarLCC(struct listacc LCC, int elem);
void borrarLCC(struct listacc LCC, int elem);
int main(void)
{
struct listacc LCC;
crearLCC(&LCC);
insertarLCC(LCC, 3);
borrarLCC(LCC, 3);
return 0;
}
La realización de la lista reorganizable aprovechando la cabecera y el centinela se deja propuesta como ejercicio.
Son listas que tienen un enlace con el elemento siguiente y con el anterior. Una ventaja que tienen es que pueden recorrerse en ambos sentidos, ya sea para efectuar una operación con cada elemento o para insertar/actualizar y borrar. La otra ventaja es que las búsquedas son algo más rápidas puesto que no hace falta hacer referencia al elemento anterior. Su inconveniente es que ocupan más memoria por nodo que una lista simple.
Se realizará una implementación de lista ordenada con doble enlace que aproveche el uso de la cabecera y el centinela. A continuación se muestra un gráfico que muestra una lista doblemente enlazada con cabecera y centinela, para lo que se utiliza un único nodo que haga las veces de cabecera y centinela.
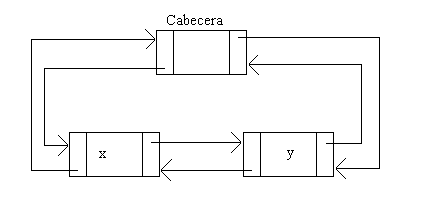
- Declaración:
struct listaDE
{
int clave;
struct listaDE *ant,
*sig;
};
- Procedimiento de creación:
void crearDE(struct listaDE **LDE)
{
*LDE = (struct listaDE *) malloc(sizeof(struct listaDE));
(*LDE)->sig = (*LDE)->ant = *LDE;
}
- Procedimiento de inserción:
void insertarDE(struct listaDE *LDE, int elem)
{
struct listaDE *actual, *nuevo;
/* busca */
actual = LDE->sig;
LDE->clave = elem;
while (actual->clave < elem)
actual = actual->sig;
/* crea */
nuevo = (struct listaDE *) malloc(sizeof(struct listaDE));
nuevo->clave = elem;
/* enlaza */
actual->ant->sig = nuevo;
nuevo->ant = actual->ant;
nuevo->sig = actual;
actual->ant = nuevo;
}
- Procedimiento de borrado:
void borrarDE(struct listaDE *LDE, int elem)
{
struct listaDE *actual;
/* busca */
actual = LDE->sig;
LDE->clave = elem;
while (actual->clave < elem)
actual = actual->sig;
/* borra */
if (actual != LDE && actual->clave == elem) {
actual->sig->ant = actual->ant;
actual->ant->sig = actual->sig;
free(actual);
}
}
Para probarlo se pueden usar las siguientes instrucciones:
struct listaDE *LDE; ... crearDE(&LDE); insertarDE(LDE, 1); borrarDE(LDE, 1);
Las listas circulares son aquellas en las que el último elemento tiene un enlace con el primero. Su uso suele estar relacionado con las colas, y por tanto su desarrollo se realizará en el tema de colas. Por supuesto, se invita al lector a desarrollarlo por su cuenta.
* Un algoritmo muy sencillo:
Se dispone de una lista enlazada de cualquier tipo cuyos elementos son todos comparables entre sí, es decir, que se puede establecer un orden, como por ejemplo números enteros. Basta con crear una lista de tipo ordenada e ir insertando en ella los elementos que se quieren ordenar al tiempo que se van borrando de la lista original sus elementos. De esta manera se obtiene una lista ordenada con todos los elementos de la lista original. Este algoritmo se llama Inserción Directa; ver Algoritmos de Ordenación. La complejidad para ordenar una lista de n elementos es: cuadrática en el peor caso (n * n) -que se da cuando la lista inicial ya está ordenada- y lineal en el mejor (n) -que se da cuanda la lista inicial está ordenada de forma inversa.
Para hacer algo más rápido el algoritmo se puede implementar modificando los enlaces entre los elementos de la lista en lugar de aplicar la idea propuesta anteriormente, que requiere crear una nueva lista y borrar la lista no ordenada.
Para hacer algo más rápido el algoritmo se puede implementar modificando los enlaces entre los elementos de la lista en lugar de aplicar la idea propuesta anteriormente, que requiere crear una nueva lista y borrar la lista no ordenada.
El algoritmo anterior es muy rápido y sencillo de implementar, pues ya están creadas las estructuras de listas ordenadas necesarias para su uso. Eso sí, en general es ineficaz y no debe emplearse para ordenar listas grandes. Para ello se emplea la ordenación por fusión de listas.
* Un algoritmo muy eficiente: ordenación por fusión o intercalación (ver Ordenación por fusión).
Problemas propuestos:
- La ordenación por fusión no recursiva: consiste en desarrollar un algoritmo para fusionar dos listas pero que no sea recursivo. No se trata de desarrollar una implementación iterativa del programa anterior, sino de realizar una ordenación por fusión ascendente. Se explica mediante un ejemplo:
3 -> 2 -> 1 -> 6 -> 9 -> 0 -> 7 -> 4 -> 3 -> 8
se fusiona el primer elemento con el segundo, el tercero con el cuarto, etcétera:
[(3) -> (2)] -> [(1) -> (6)] -> [(9) -> (0)] -> [(7) -> (4)] -> [(3) -> (8)]
queda:
2 -> 3 -> 1 -> 6 -> 0 -> 9 -> 4 -> 7 -> 3 -> 8
se fusionan los dos primeros (primera sublista) con los dos siguientes (segunda sublista), la tercera y cuarta sublista, etcétera. Observar que la quinta sublista se fusiona con una lista vacía, lo cual no supone ningún inconveniente para el algoritmo de fusión.
[(2 -> 3) -> (1 -> 6)] -> [(0 -> 9) -> (4 -> 7)] -> [(3 -> 8)]
queda:
1 -> 2 -> 3 -> 6 -> 0 -> 4 -> 7 -> 9 -> 3 -> 8
se fusionan los cuatro primeros con los cuatro siguientes, y aparte quedan los dos últimos:
[(1 -> 2 -> 3 -> 6) -> (0 -> 4 -> 7 -> 9)] -> [(3 -> 8)]
queda:
0 -> 1 -> 2 -> 3 -> 4 -> 6 -> 7 -> 9 -> 3 -> 8
se fusionan los ocho primeros con los dos últimos, y el resultado final es una lista totalmente ordenada:
0 -> 1 -> 2 -> 3 -> 3 -> 4 -> 6 -> 7 -> 8 -> 9
3 -> 2 -> 1 -> 6 -> 9 -> 0 -> 7 -> 4 -> 3 -> 8
se fusiona el primer elemento con el segundo, el tercero con el cuarto, etcétera:
[(3) -> (2)] -> [(1) -> (6)] -> [(9) -> (0)] -> [(7) -> (4)] -> [(3) -> (8)]
queda:
2 -> 3 -> 1 -> 6 -> 0 -> 9 -> 4 -> 7 -> 3 -> 8
se fusionan los dos primeros (primera sublista) con los dos siguientes (segunda sublista), la tercera y cuarta sublista, etcétera. Observar que la quinta sublista se fusiona con una lista vacía, lo cual no supone ningún inconveniente para el algoritmo de fusión.
[(2 -> 3) -> (1 -> 6)] -> [(0 -> 9) -> (4 -> 7)] -> [(3 -> 8)]
queda:
1 -> 2 -> 3 -> 6 -> 0 -> 4 -> 7 -> 9 -> 3 -> 8
se fusionan los cuatro primeros con los cuatro siguientes, y aparte quedan los dos últimos:
[(1 -> 2 -> 3 -> 6) -> (0 -> 4 -> 7 -> 9)] -> [(3 -> 8)]
queda:
0 -> 1 -> 2 -> 3 -> 4 -> 6 -> 7 -> 9 -> 3 -> 8
se fusionan los ocho primeros con los dos últimos, y el resultado final es una lista totalmente ordenada:
0 -> 1 -> 2 -> 3 -> 3 -> 4 -> 6 -> 7 -> 8 -> 9
Para una lista de N elementos, ordena en el mejor y en el peor caso en un tiempo proporcional a: N·logN. Observar que para ordenar una lista de 2 elementos requiere un paso de ordenación, una lista de 4 elementos requiere dos pasos de ordenación, una lista de 8 elementos requiere tres pasos de ordenación, una lista de 16 requiere cuatro pasos, etcétera. Es decir:
log 2 = 1
log 4 = 2
log 8 = 3
log 16 = 4
log 32 = 5
De ahí el logaritmo en base 2.
N aparece porque en cada paso se requiere recorrer toda la lista, luego el tiempo es proporcional a N·logN.
Se pide: codificar el algoritmo de ordenación por fusión ascendente.
Las listas enlazadas son muy versátiles. Además, pueden definirse estructuras más complejas a partir de las listas, como por ejemplo arrays de listas, etc. En algunas ocasiones los grafos se definen como listas de adyacencia (ver sección de grafos). También se utilizan para las tablas de hash (dispersión) como arrays de listas.
Son eficaces igualmente para diseñar colas de prioridad, pilas y colas sin prioridad, y en general cualquier estructura cuyo acceso a sus elementos se realice de manera secuencial.
No hay comentarios:
Publicar un comentario